Tax

Memory limit: 128 MB

The king of Byteland decided to follow a worldwide trend and introduce taxes everywhere he can. His new invention is the so-called travel tax that is paid by everyone travelling through the country.

Each Bytean road is assigned a tax rate. When passing through a town one needs to pay a tax that equals the maximum of the tax rate on the road that was used to enter the town and of the tax rate on the road that was used to exit the town. One also pays the tax in the first and the last town on the trip: there the tax amount equals the rate of the only corresponding road of the trip.

Your friend Byteasar is going for a trip from Bytetown to Bitcity. Help him plan his trip so that the amount of tax he pays is minimal.

Input

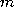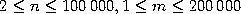The first line of input contains two integers and (), the number of towns and the number of roads in Byteland. The towns are numbered 1 through .

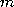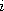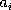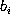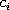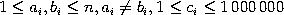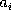The following lines contain descriptions of roads. The -th of those lines contains three integers , , (). This means that the towns and 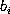are connected by a bidirectional road with the tax rate equal to 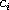bythalers. Each pair of towns is connected by at most one road.

Output

The first and only line of output should contain one integer: the minimal tax amount (in bythalers) on a trip from Bytetown (i.e. the town number 1) to Bitcity (i.e. the town number ). You can assume that in each input data there is a sequence of roads connecting these two towns.

Example

For the input data:

4 5
1 2 5
1 3 2
2 3 1
2 4 4
3 4 8

the correct result is:

12

Explanation of the example: The optimal trip leads through the towns 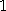, , 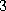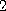and . The tax amount paid in the respective towns is: 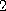, , 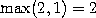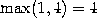and . This yields 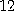bythalers of tax in total.

Task author: Jakub Lacki (and friends).